- Calculating Tension.
- Calculating Centripetal force.
- Calculating centripetal acceleration.
- Calculating scalar and angular velocities.
- And calculating period and frequency.
Let’s first begin with some short descriptions and formulas.
When an object is travelling in a circular motion its direction is changing continually, this results in a change in velocity it also follows that any change in velocity causes acceleration and for an acceleration to take place a force is needed. The force present when a body is moving in a circular motion is known as centripetal force, this force acts towards the center of motion.
It is also said that the centripetal acceleration must move in the same direction as the centripetal force, therefore it also acts toward the center of motion. The formulas below show the relationship between centripetal acceleration and angular and scalar velocity:
To read more about angular and scalar velocity click here.
Example #1
The pendulum above has a mass of 2kg. The pendulum is moving in a horizontal circle. The string is inclined at 30 degrees to the vertical.
- Calculate the tension in the string
- Calculate the centripetal force.
- Calculate the centripetal acceleration.
- Calculate Scalar & angular velocities.
- Calculate period & frequency of centripetal motion.
Answers:
First before we begin answering the question we need to make some additions to the drawing above. We want to work with an angle besides the 30 degrees if you look at the diagram you’ll realize there’s a triangle but one of the angles are missing, this is the angle we want to use. You can easily find this angle because you are already given one angle (30 degrees) and since it is a right angled triangle (indicated by the box formed between the vertical and horizontal line)it also has 90 degrees, therefore the remaining angle must be 60 degrees, if we were to add them all up we would get a total of 180 degrees. So place the 60 degrees in the missing position. The question also stated that you would need to calculate tension, so you would need to split the “T” in its horizontal and vertical components. This would give “T × sin 60” for the vertical component and “T × cos 60” for the horizontal component. Now place these components in the diagram. The next thing to note is that the pendulum has a mass 2kg therefore a downward force of weight must be acting on the body, add this as well to the diagram.
The resulting diagram would be:
- To answer the first question which asked for the tension in the string we use the vertical component but if you look closely you will see that there is weight also acting downward against the vertical component so we use the rule:
- Calculating centripetal force. Remember as stated above that this is the force acting toward the center. Therefore if you look at the diagram you will realize that the horizontal component ( T × cos 60)is the one acting toward the center. This would give:
- Calculating centripetal acceleration. Remember this moves in the same direction of the force and you’re also given mass so all you have to do is transpose this formula to find acceleration:
- In this question they asked for the scalar and angular velocities. The formula that relates these to centripetal acceleration was given above:
- Calculating period:
Centripetal force = T × cos 60
= 23.9 × 0.5
= 11.55N
Where r is the radius











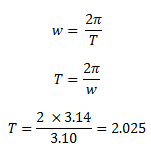








15 Response to Calculating Circular Motion: Questions & Answers
Awesome explanation. It shows that you love what you are studying and that you want to share your passion with others.
WOw! awesome, the explanation is just too interesting to be true but it is true,it is just great.
A satellite orbits the earth with a distance of (1.5x10^7)m above the planets surface and takes 8.65 hr for each revolution about the earth. The earths radius is (6.38x10^6 )m. What is the centripetal acceleration of this satellite?
WOw! awesome, the explanation is just too interesting to be true but it is true,it is just great.
WOw! awesome, the explanation is just too interesting to be true but it is true,it is just great.
I can't stop clapping for it. The explanations is wonderful and sequential
That is good it help
Ankara
Antalya
istanbul
Ordu
izmir
M4ZZ
https://titandijital.com.tr/
denizli parça eşya taşıma
sinop parça eşya taşıma
artvin parça eşya taşıma
antep parça eşya taşıma
FDAİ8
A2B04
Iğdır Şehir İçi Nakliyat
Kütahya Lojistik
Karabük Şehir İçi Nakliyat
Ardahan Evden Eve Nakliyat
Niğde Şehir İçi Nakliyat
Konya Şehirler Arası Nakliyat
Karapürçek Parke Ustası
Bartın Evden Eve Nakliyat
Burdur Lojistik
51D1A
Adıyaman Şehir İçi Nakliyat
Kilis Şehir İçi Nakliyat
Aksaray Şehirler Arası Nakliyat
Çerkezköy Oto Lastik
Tekirdağ Parke Ustası
Adıyaman Parça Eşya Taşıma
Cointiger Güvenilir mi
Hakkari Şehir İçi Nakliyat
Çerkezköy Çilingir
Thanks greaat post
880EEEEA66
ucuz tiktok takipçi
AD92D76221
bot takipçi
twitter beğeni satın al
instagram takipçi
ucuz takipçi
takipçi
95F74D8E2C
bot takipçi instagram
tiktok beğeni satın al
instagram takipçi
takipçi
bot takipçi
Post a Comment
Have a Question or a Comment?