What is Diffraction?
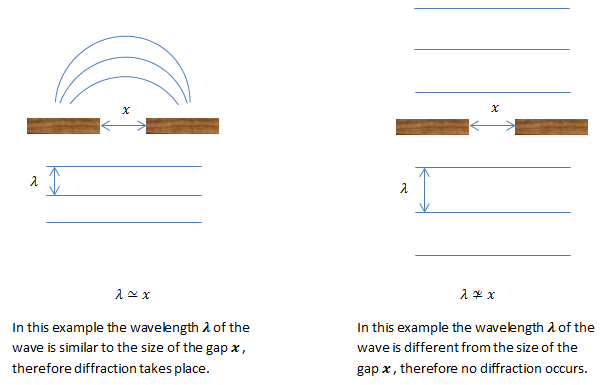
By definition diffraction is the spreading out or scattering of waves as they pass through gaps. However certain conditions must be present for a wave to be diffracted when passing through a gap, the length of the wave and the size of the gap has to be the same or almost the same.

What is Interference?
Interference is what occurs when two or more waves interact with each other producing another wave.

Types of Interference?
There are two types of interference these are:

1. Constructive Interference
2. Destructive Interference

Constructive Interference
In constructive interference, when the waves interfere a larger wave is produced, this is as a result of the waves meeting at in-phase points such as a crest meeting a crest or a trough meeting a trough.

Destructive Interference
In destructive interference the two original waves will meet to produce a smaller wave. The final wave produced is as a result of the original waves meeting at out of phase points such as a crest meeting a trough. The resulting wave can also be non-existent.

Diffraction – Interference Fringes

In the diagram above diffraction occurs at slits s1 and s2, the diffracted waves then interfere. The solid lines in the diagram represent crests; therefore in the diagram above the waves interfere at in-phase points (crest to crest) producing bright fringes or bands. In this diagram constructive interference takes place.

In the diagram above diffraction occurs at slits s1 and s2, the diffracted waves then interfere producing dark bands on the screen. This is known as destructive interference and occurs as a result of the waves interfering at out of phase points (crest to trough), the crest is represented by the solid line while the trough is represented by the broken line.

In some waves the vibrations can be observed moving throughout the material but in others the vibrations/ disturbances can appear to be still or not present in the material; with these facts scientists were able to categorize waves based on these differing characteristics. These are:

1. Progressive Waves
2. Standing/Stationary Waves

Progressive Waves
Progressive waves are those waves having visible disturbances meaning the vibrations can be seen moving throughout the material.

Standing/Stationary Waves
Standing waves are produced when two waves interfere this results in an invisible disturbance though the wave is moving throughout the material. Standing waves consist of two different points known as nodes and antinodes.

Nodes: These are points in the wave that have zero energy and displacement.
Anti-Nodes: These are points in the wave that have the highest energy or amplitude.

The distance between two consecutive nodes or anti-nodes makes half a wavelength.

Waves formed from stringed and wind instruments are stationary waves. Open ends always have an antinode while closed ends have a node.

Stationary wave in Wind Tube

What are In-Phase Points?
Inphase points are points of a wave that are located at the same position in the wave cycle. Waves that are inphase are separated by an even multiple of half wavelength (π).Such waves will undergo constructive interference.

Inphase

The x’s in the diagram above marks points that are in-phase in the wave cycle.

What are Out of Phase Points?
Out of phase points are points that are not located in the same position in the wave cycle. Waves that are out of phase are usually separated by an odd multiple of half wavelengths (π). These waves undergo destructive interference.

Looking at the diagram above we are going to determine which are in phase against those that are out of phase.

1. π to 3π would be inphase because the difference is an even number 2π.
2. 2π to 4π would be inphase because the difference is also an even number 2π.
3. 2π to 6π would be inphase because the difference is an even number 4π.
4. 1π to 4π would be out of phase because it is separated by an odd number 3π.

What is Longitudinal Wave?
A longitudinal wave is one in which the particles in the wave vibrate parallel to the direction in which the wave is moving. That is the particles can only move in a back or forth movement in the same direction as the wave.

Examples of Longitudinal Waves:

1. Sound Waves
2. Waves in Springs
3. Vibrations in Gases
4. Waves in Tsunami

Longitudinal wave

What is Transverse Wave?
A transverse wave is one in which the particle vibrates perpendicularly to the direction in which the wave is moving. Such waves can only move in an up or down direction with respect to the direction of the wave.

Examples of Transverse Waves?

1. Water Waves
2. Waves in Ropes
3. Electromagnetic waves
4. Guitar string that is Vibrating

Transverse Wave

Ant

Many of us should probably know by now that an ant is one of the hardest working creatures on the planet. Just observing an ant’s activity can give one the impression that they never rest, but is that really true?
Before we begin answering this question let’s start by answering this one:

Can any living thing survive without rest?
The obvious answer to this is no. No living organism can survive without resting, resting allows us to regain energy and being as hard working as an ant must mean that allot of resting is needed. Therefore the obvious answer to the primary question is YES an ant does rest.

So what’s the trick to it?

1. They all look alike
2. They are organized
3. You really didn’t observe that much.

Seeing that all worker ants look alike it’s impossible to tell who is/isn’t working and since ants are organized workers, they work together, some may work at a particular time in the day and some at another time so they are able to rest at different intervals just like us humans.
Need proof? Then watch the video below of ants that are sleeping:

Wave
via ScienceTm

In previous lessens we looked at what is a wave. If you’re unclear on this topic click here to read more about waves.
In physics there are two known types of waves, these are:

1. Mechanical Wave
2. Electromagnetic wave

The differences between these two lie in their means of transferring energy. One may not see the difference between sound waves and light rays because as humans we aren’t capable of seeing such things with our naked eyes but thanks to human intelligence and through many research scientists were able to detect movement of energy in waves and thus differentiate the means by which they are transferred.

What are Mechanical Waves?
Mechanical waves are those that need a material medium with particles to enable them to move. Therefore these waves can’t “travel on their own”.

Examples of mechanical waves:

• Sound Waves
• Water Waves
• Waves in springs

What is Electromagnetic wave?
Electromagnetic waves are those that do not need any material medium to enable them to move. Therefore these waves can travel on their own. These waves can travel through a vacuum.

Examples of electromagnetic waves:

• Visible light
• X-rays
• Infrared rays
• Ultraviolet rays
• Radio waves

Earth Image
via wikipedia

What is Gravitational Field Strength?

The gravitational field strength at any point can be defined as the force per unit mass placed at the point in the field.
Formula for Gravitational field strength:

Gravitational Field Strength

What is Geostationary Orbit?
Geostationary orbit refers to a body orbiting a fixed position above the earth. For example a satellite moving with geostationary orbit around the earth has to have the same period of rotation as the earth (24hrs) therefore allowing it to remain above the same geographic area on the earth.

What is Escape Velocity?
Escape velocity refers to the minimum velocity a body needs to escape the gravitational pull of the earth.

Formula for escape velocity:

Escape velocity

Where:
V is escape velocity
G is universal gravitational constant
me is mass of the earth
re is radius of the earth

In previous lessons we spoke about simple harmonic motion, its definition, systems that engage in simple harmonic motion and formulas involved. Now we’ll be looking at calculating Simple harmonic motion questions.

Example # 1

S.H.M

In the diagram above a particle is moving with S.H.M with a period of 24 seconds between two points A and B. Find the time taken to travel from:
a) A to B
b) O to B
c) O to C
d) D to E

Answers:
Note that the period is the time taken to complete one revolution in this case the period is the time taken for the particle to travel from A to B and then to A again (24 seconds as stated in the question above).

a) A to B
A to B is half a period which would be = 12 second

If you want to work this question in a more detailed way, you can do this:

Distance from A to B to A again = 16m
Distance from A to B = 8m
Period (A to B to A again) = 24 seconds
Time (t) from A to B =???

b) O to B
O to B is quarter of the period so the answer would be = 6 sec

Or you can follow the above pattern:

Distance from A to B to A again = 16m
Distance from O to B = 4m
Period (A to B to A again) = 24 seconds
Time (t) from O to B =???

c) O to C
This is one eight of the period which would be = 3 seconds

Or by detailed calculation:

Distance from A to B to A again = 16m
Distance from O to C = 2m
Period (A to B to A again) = 24 seconds
Time (t) from O to C =???

d) D to E
Note with this question, if you observe the diagram carefully you will see that you weren’t given the distance between D to E directly. However this can easily be found by subtracting the distance O to D from the distance O to E and this would give you the distance from D to E.

Distance from A to B to A again = 16m
Distance from D to E = 3.5 – 3 = 0.5m
Period (A to B to A again) = 24 seconds
Time (t) from D to E =???

What is Simple Harmonic Motion?
Simple Harmonic Motion can be defined as the motion of an object where its acceleration is directly proportional to its distance from a fixed point along a path. The acceleration is said to always be directed towards the fixed point. This fixed point is known as the equilibrium position; this is because it is where the object that is swinging freely would come to rest given that it has lost all its energy.

The diagram below shows a pendulum in simple harmonic motion:

Pendulum in S.H.M

Where:
P is the equilibrium position (where the body would come to rest)
PQ & PR gives the amplitude position which is the greatest displacement from equilibrium position.
X is the position from the equilibrium position.

When the object is swinging freely you’ll probably realize that it moves faster when passing through its equilibrium position P, this is because the body’s acceleration and velocity is greatest as it passes through the equilibrium position. Also the opposite happens as the body leaves the equilibrium position, the acceleration and velocity lessens as the body’s position, x, moves further away from the equilibrium position.

Formulas involved in simple harmonic motion:

S.H.M formulas

The diagram below shows a spring in simple harmonic motion:

Spring in S.H.M

From the previous article we looked at circular motion, its definition, formulas involved, types of velocities etc. Now we will look at different calculations involving circular motion. This tutorial is intended to give you a well-rounded understanding on how to calculate different variables involved in circular motion questions namely:

• Calculating Tension.
• Calculating Centripetal force.
• Calculating centripetal acceleration.
• Calculating scalar and angular velocities.
• And calculating period and frequency.

Let’s first begin with some short descriptions and formulas.
When an object is travelling in a circular motion its direction is changing continually, this results in a change in velocity it also follows that any change in velocity causes acceleration and for an acceleration to take place a force is needed. The force present when a body is moving in a circular motion is known as centripetal force, this force acts towards the center of motion.

It is also said that the centripetal acceleration must move in the same direction as the centripetal force, therefore it also acts toward the center of motion. The formulas below show the relationship between centripetal acceleration and angular and scalar velocity:

To read more about angular and scalar velocity click here.

Example #1

The pendulum above has a mass of 2kg. The pendulum is moving in a horizontal circle. The string is inclined at 30 degrees to the vertical.

1. Calculate the tension in the string
2. Calculate the centripetal force.
3. Calculate the centripetal acceleration.
4. Calculate Scalar & angular velocities.
5. Calculate period & frequency of centripetal motion.

Answers:
First before we begin answering the question we need to make some additions to the drawing above. We want to work with an angle besides the 30 degrees if you look at the diagram you’ll realize there’s a triangle but one of the angles are missing, this is the angle we want to use. You can easily find this angle because you are already given one angle (30 degrees) and since it is a right angled triangle (indicated by the box formed between the vertical and horizontal line)it also has 90 degrees, therefore the remaining angle must be 60 degrees, if we were to add them all up we would get a total of 180 degrees. So place the 60 degrees in the missing position. The question also stated that you would need to calculate tension, so you would need to split the “T” in its horizontal and vertical components. This would give “T × sin 60” for the vertical component and “T × cos 60” for the horizontal component. Now place these components in the diagram. The next thing to note is that the pendulum has a mass 2kg therefore a downward force of weight must be acting on the body, add this as well to the diagram.

The resulting diagram would be:

1. To answer the first question which asked for the tension in the string we use the vertical component but if you look closely you will see that there is weight also acting downward against the vertical component so we use the rule:

2. Calculating centripetal force. Remember as stated above that this is the force acting toward the center. Therefore if you look at the diagram you will realize that the horizontal component ( T × cos 60)is the one acting toward the center. This would give:


Centripetal force = T × cos 60 
= 23.9 × 0.5 
= 11.55N


3. Calculating centripetal acceleration. Remember this moves in the same direction of the force and you’re also given mass so all you have to do is transpose this formula to find acceleration:





4. In this question they asked for the scalar and angular velocities. The formula that relates these to centripetal acceleration was given above:


Where r is the radius

Since we weren’t given the value of the radius we would have to find it first before we can find either scalar or angular velocity. Assuming we all can identify the radius on the diagram let’s use the formula:



If you look at the triangle formed on the circle you would notice that the adjacent would be the radius and the hypotenuse would be the 1.2m. Therefore:

Calculating scalar velocity:

Calculating angular velocity:

5. Calculating period:

Calculating frequency:

Lying Person:
Image by bvonmoney

Are you tired of being lied at, maybe by a friend, family, spouse etc. and you’re absolutely certain they’re lying and just can’t prove it? well you’re at the right place, here I’ll be showing you different ways/methods of detecting instances where a person maybe lying. Though these methods may not be exact and can be manipulated by “expert liars”, they still have proven to be effective. Below are the different methods to know when someone is lying:

• Using reaction time and facial expressions.
Often times you’ll see individuals react in the appropriate way depending on the condition but what you may also see is that their facial expressions usually delay their speech, for example a lying person receiving sad news may respond “Oh that’s so sad” but if you watch closely you’ll realize there’s a delay in their facial expression of sadness. Emotions that are true on the other hand are most times instantaneous.
• Changing the Subject
This is probably one of the most obvious and most used methods by liars. At some point in time you may be speaking to someone about a particular situation and all of a sudden the person changes the subject, this is an indication that the person is uncomfortable with the conversation possibly because they’re lying. A truthful person on the other hand wouldn’t stray from the topic and would probably try to regain focus on the topic.
• Using the eye direction.
  
This is a very effective way of telling that someone is lying, and is used by many police officers. As long as you can remember the directions there shouldn’t be any problem telling whether or not a person is lying. When a person looks to their right (your left), this is an indication that the person is constructing an event, while on the other hand if they look to their left (your right), this indicates that the person is actually remembering something. So simply put if the person looks to their right when answering a question he/she is actually making up something (lying) but if he/ she looks to their left this means that they are actually remembering something(telling the truth).

You can also watch the video below by Dr. Lillian Glass on more ways to detect a lying person:

What is Circular Motion?
Circular motion refers to motion along a circular path or circular orbit.

Two types of velocities take place when an object is moving in circular motion these include Scalar velocity (υ) and Angular Velocity (ω).


Scalar Velocity (υ)
Scalar velocity can be defined as the velocity occurring around the circumference of the circle formed by the path.

Angular Velocity (ω)
Angular velocity can be defined as the rate of turn of the angle present at the center of the circle.

Angular Velocity

The formula below shows the relationship between angular and scalar velocity:
υ= ωr

Period (T)
Period can be defined as the time taken for an object to complete one revolution. The formula below shows the relationship between angular velocity and period:

Angular Velocity and Period

Frequency(F)
Frequency can be defined as the number of revolutions per second. It is said to be the inverse of period:

Frequency and Period of rotation

Circular Motion

Are they the same?
Many persons get confused when they hear about center of mass and center of gravity because they both sound the same. However the truth is they may or may not coincide depending on certain conditions. These conditions include whether or not they are in a uniform or non-uniform gravitational field. When in a uniform gravitational field they do coincide but when they are not in a uniform gravitational field they are treated differently. You can click here to see a complete explanation of the differences between these two.

Center of Mass:
The center of mass is that point of an object where all its mass appears to be located.

Center of Gravity:
The center of gravity of an object is that point at which all the gravity force appears to be acting, but in reality gravity acts on all points of the object.

Center of Mass Center of Gravity

The video below shows an animation outlining the center of mass of different objects.

What is Energy?
Energy can be defined as the capacity to do work.

Types of Energy


Mechanical Energy: - By definition mechanical energy is the sum of Kinetic energy(K.E) and Potential energy(P.E).

Mechanical energy = Kinetic Energy + Potential Energy

Kinetic Energy: - Kinetic energy is the energy due to a body’s motion.

K.E = 1/2 mass × velocity²

Potential Energy: - Potential Energy is energy due to a body’s position or condition.

P.E = mass × gravity × height

Law of Conservation of mechanical energy
In a system where only forces associated with potential energy are acting (gravitational/ elastic), the sum of the Kinetic and Potential energies is constant.

K.E + P.E = Constant

These conditions exist for any object rising of falling above the earth’s surface:

1. For a body that is rising:

Loss in K.E = Gain in P.E

     2.  For a body falling towards the earth:

Loss in P.E = Gain in K.E

What is Equilibrium?
When a system is said to be in equilibrium this means it is in balance and is either moving at constant velocity motion or is at rest.

Situations that must exist for a system to be at equilibrium:

1. The resultant force in any direction must be zero.
2. The total moments of the system must be zero. Meaning:

Clockwise Moments = Anti- Clockwise Moments

How to calculate equilibrium?


Example 1
If the system below is in equilibrium find the unknown force “F”.

System in equilibrium

Step 1
In the question they stated that the system is in equilibrium, therefore you can go ahead and use the equation:

Clockwise Moments = Anti-Clockwise Moments

But remember that formula for moments is:
Force × Perpendicular distance from pivot

Therefore:

Clockwise Force × Perpendicular distance = Anti-clockwise Force × Perpendicular Distance

Step 2
Identify the forces in the system that are moving clockwise and anti-clockwise with their respective perpendicular distances, and then substitute those values in the above equation:

After substituting the values above into the formula you should get:

Clockwise Moments = Anti-Clockwise Moments

Clockwise Force × Perpendicular distance = Anti-clockwise Force × Perpendicular Distance

F × 8m = 120N × 6m

Step 3
After placing the values into the formula all that is left to do is transpose the formula to make “F” the subject then solve for “F”. The overall calculation would then be:

Calculating Equilibrium